時系列分析とは〜基本的な分析方法について〜

時系列分析とは

時系列分析は、「時間とともに変化するデータ」を理解し、予測するための方法です。
具体的には過去のデータを使って未来を予測したり、時間とともに記録されたデータの傾向やパターンを探ることを目的としています。

日常での例

例えば、家計簿をつけているとしましょう。毎月の支出を記録していくと、「食費はだいたい毎月どのくらいかかるか」とか、「冬になると光熱費が増える」といったパターンが見えてきます。
この「パターンを見つけて、次に何が起こるかを予測する」というのが、時系列分析の基本的な考え方です。

なぜ時系列分析が重要なのか？

そもそも、時系列のデータというのは日常や業務のシーンで頻出であると言えます。
例えば、スーパーの売上実績なら、購入品目や値段といった情報と共に日時を記録するのが普通ですし、より一般的なデータの例として天気などの情報も日時情報がないと何の役にも立たないデータであると言えます。
そういったさまざまなデータに対して、役に立つ分析の切り口として時系列分析が活躍します。たとえば、次のようなシチュエーションで力を発揮します。

• 予算の計画: 来年の売上を予測して、どれくらいの予算が必要かを決める。
• 在庫管理: いつ、どれくらいの在庫が必要かを予測して、無駄なコストを削減する。
• 家計管理: 毎月の支出を分析して将来の出費を予測して、計画的な貯金をする。

これらは、業務上の応用においても重要ですし、個人の生活でも役に立ちます。

時系列データの4つの主な変動成分

さて、時系列データの分析の第一歩として、時系列データの変動成分について学びましょう。
時系列データは一般的に、以下の4つの変動成分に分解することができます。

• T：趨勢変動成分
• C：循環変動成分
• S：季節変動成分
• I：不規則変動成分

これら4つの和や積で元の時系列データ(以下、現系列と呼ぶ)を表す事でデータの解釈性を高めて、全体の変動要因を探ったり予測精度を高めるアプローチに繋げることができます。
以下に各成分の詳細をまとめます。

1. トレンド成分（T: Trend）

トレンドは、データが長期間にわたって増えたり減ったりする傾向のことです。簡単に言えば、データが全体的に上がっているのか下がっているのかを見る部分です。

実務の例:
例えば、ある会社の売上データを見たとき、毎年少しずつ売上が増えているなら、それが「トレンド」です。このトレンドを把握すれば、将来的に売上がどうなるかを予測しやすくなります。

2. 循環成分（C: Cycle）

循環成分とは、データに見られる規則的だけど一定ではない上下の動きのことです。景気の良し悪しで売上が上下するようなパターンを指します。

実務の例:
例えば、不況のときには売上が減り、景気が良くなると売上が増えるパターンが見られる場合です。このような動きを知っていれば、景気が悪くなる前に対策を取ることができます。

3. 季節成分（S: Seasonality）

季節成分は、年中行事や季節の変化に伴う規則的なデータの変動です。たとえば、夏にはアイスクリームがよく売れ、冬には暖房器具が売れるような動きがこれに当たります。

実務の例:
小売業では、クリスマスやお正月に向けて売上が増えることがよくあります。これを知っていれば、その時期に向けて在庫を増やすなどの対応ができます。

4. 不規則成分（I: Irregularity）

不規則成分は、予測できないランダムなデータの動きです。例えば、突然の自然災害や予期せぬイベントによる影響がこれに当たります。

実務の例:
自然災害で工場が一時的に止まり、売上が急に落ちたとき、その影響は不規則成分と考えられます。これは予測が難しいので、データ分析では無視されることが多いです。

これら4つの変動成分のうち実応用上はT（趨勢変動成分）とC（循環変動成分）をまとめて、TC（趨勢循環変動）とすることが多いです。
解釈としては、TCは長期的な上昇または下降の動きであるとしてトレンド成分という扱いをすることがになります。

---

3つの特徴把握方法

さて、実際に時系列データを入手したときにまず行う3つの基本的な分析手法を順に見てみましょう。

1. 時系列データの変動成分を分解してみる

先ほど説明したように時系列のデータは、トレンド（長期的な傾向）、季節性（周期的な変動）、残りの予測できない部分(ノイズ)に分けられます。これによってデータがどのように動いているのか、解釈性が高まります。

実際にPythonを使った変動成分分析の一例を見てみましょう。

ステップ:

1. データをグラフにして、全体の傾向を確認します。
2. statsmodelsのseasonal_decompose や STL というツールを使ってデータを分解します。
3. 分解したデータを再度グラフ化して、どの部分がトレンドで、どの部分が季節性かを確認します。

また、今回はアメリカの国際線乗客者数の月次推移データを使用します。
変動成分分析のサンプルとしてよく例に挙げられるデータで、seabornで用意されているサンプルデータセットの中にも含まれているためすぐに実験できるのが良いです。
ステップを順に見ていきましょう。

1. データをグラフにして、全体の傾向を確認します。

まずはデータの概観を掴むために、先頭五行とグラフを表示してみます。

コード例:

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

# 表の確認
flights = sns.load_dataset("flights")
print(flights.head())

# 折れ線グラフの作成
flights.passengers.plot()
plt.show()

出力:

year	month	passengers
0	1949	Jan	112
1	1949	Feb	118
2	1949	Mar	132
3	1949	Apr	129
4	1949	May	121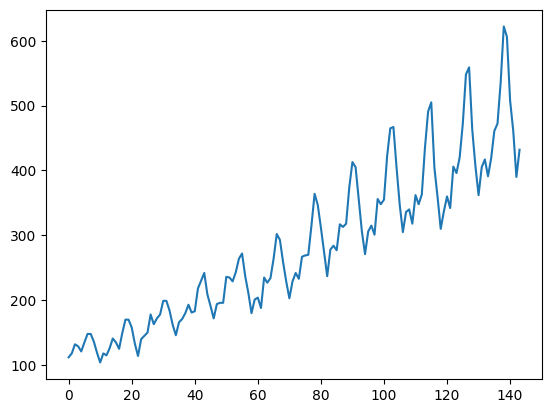

この結果から分かることは、今回のデータflightsは

• ‘year’, ‘month’, ‘passengers’という3つの列で構成されている
• 徐々に乗客数は増加傾向にありそう
• 季節による増減周期がありそう

といったことが読み取れるかと思います。
このうち、1ポチ目は見たままの事実なので、2,3ポチ目を以下2ステップ目のデータ分解をおこなって確かめていきましょう！

2. statsmodelsのseasonal_decompose や STL というツールを使ってデータを分解します。

コード例:

from statsmodels.tsa.seasonal import seasonal_decompose

# 加法モデルでのデータ分解
result = seasonal_decompose(flights['passengers'], model='additive', period=12)
result.plot()

出力:

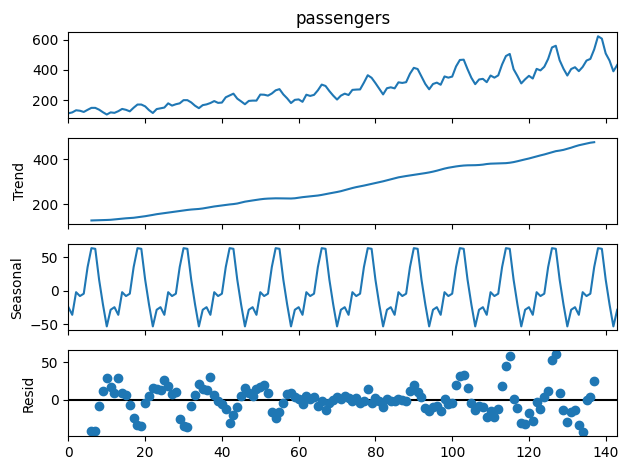
この出力の読み方ですが、まず一番上は元のグラフ、そして上から順にTC (トレンド成分)、S (季節成分)、残差といった順で並んでいます。
トレンドは上昇傾向、季節の周期も一定の形状が存在することが読み取れますね。
続いて、STLを使った分解の例です。

コード例:

from statsmodels.tsa.seasonal import STL

# STLでの分解
stl = STL(flights['passengers'], period=12).fit()
stl.plot()

出力例:

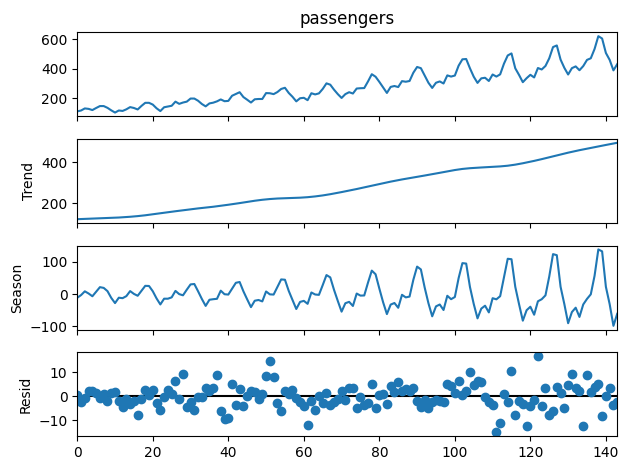
こちらもグラフの読み方はseasonal_decomposeと同様です。
ちなみにSTLではLoess平滑化という技術が使われていて、外れ値に強いという特徴があります。

また、seasonal_decomposeでもSTLでもperiod=12という引数が指定されていますが、これは周期を指定するもので、今回は1年を1単位とした周期が見られるという見込みのもと設定したものです。

2. データが「定常」かどうかを確認する

「定常」というのは、そのデータの統計的な特性が時間によって変わらない状態を指します。
平均や分散、自己相関が時間に依らず一定であることが「定常」であるための必要条件と言えます。
さて、この定常性は時系列データの予測に関係してきます。
どういう事かというと、逆説的な言い回しですが「定常」でない↔︎時間が進むにつれ統計的特性が変わってしまうという事なので、過去のデータから算出した統計的特性が未来では全く役に立たないという事になります。
そこで、定常であることが時系列データの予測信頼性を上げるということになるのです。

では、「定常」に関わる時系列データの前処理ステップを見てみましょう。

ステップ:

1. ADFという検定を使ってデータが定常かどうかをチェックします。
2. データが定常でない場合、対数変換や差分化という方法でデータを安定させます。

まず、定常であることの確認にはADF検定と呼ばれる判定を行います。
これは単位根と呼ばれる、非定常であるか否かを測る統計的な証拠の一つをデータが持っているかを判定する検定で、ここで非定常であると判定した場合には続く「定常化」の操作を行います。

「定常化」とは非定常のデータを変換して定常にする操作のことで、具体的には差分を取ったり対数変換を行うといった操作が行われます。

さてこれらの定常判定と、定常化のステップをコードで実装してみましょう。

コード例:

from statsmodels.tsa.stattools import adfuller

print("定常化前"）
result = adfuller(flights['passengers'])
print('ADF Statistic:', result[0])
print('p-value:', result[1])

# 対数変換と差分化
df_log = np.log(flights['passengers'])
df_diff = df_log.diff().dropna()

# 定常化後のADF検定
print("¥n定常化後")
result = adfuller(df_diff)
print('ADF Statistic:', result[0])
print('p-value:', result[1])

出力:

差分化前
ADF Statistic: 0.8153688792060498
p-value: 0.991880243437641

差分化後
ADF Statistic: -2.717130598388114
p-value: 0.07112054815086184

結果の解釈ですが、その前にADF検定では何を見ているかを説明します。
ADF検定では帰無仮説として「時系列データに単位根が存在し、データが非定常である」という設定のもと検定を行います。
ADF検定の出力はいくつかの要素で構成されますが、今回見ているのは

• ADF統計量
• p値

の2つとなります。
ADF統計量は簡単に言えば、データが非定常である可能性の高さを示す値です。
一方のp値は通常の統計的仮説検定でもよく見る値ですが、帰無仮説(否定したい仮説)が正しいという前提のもとで、観測された結果が得られる確率です。一般的には5％以下である場合は帰無仮説を棄却します。

今回の結果では定常化前はADF統計値もp値も高いため、(帰無仮説は棄却せず)データは非定常であると言えます。一方で、定常化後はADF統計値もp値も高いため、(帰無仮説は棄却せず)データは非定常であると言えます。

3. データの自己相関をチェックする

「自己相関」というのは、データが過去のデータとどれくらい似ているかを見るものです。これを確認することで、どの遅れ（ラグ）がデータに影響を与えているのかが分かります。
この時の指標は「自己相関係数」と呼び、元のデータとずらしたデータの相関係数を取ります。
そして、ずらした時間分（ラグ）=1,2,・・・に対して、それぞれ自己相関係数を計算してグラフにしたものを「コレログラム」と呼びます。
また、さらに正確に相関を確認したい場合は偏自己相関係数という値を確認します。例えば先ほどのコレログラムを見て12ヶ月ごとに周期がありそうとしたときに、これは実は11ヶ月前のデータの影響を受けている事があります。偏自己相関係数ではこういった関係性を排除して12ヶ月前のデータとの直接的な関係を計算できます。

先ほどの差分化操作をおこなって得られたデータに対して、自己相関の確認を行ってみましょう。

ステップ:

1. コレログラムを使って、データの自己相関を視覚化します。
2. 偏自己相関のグラフを使って、特定の遅れがデータにどう影響しているかを確認します。

コード例:

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

plot_acf(df_diff)  # コレログラムの描画
plot_pacf(df_diff)  # 偏自己相関係数の描画
plt.show()

出力：

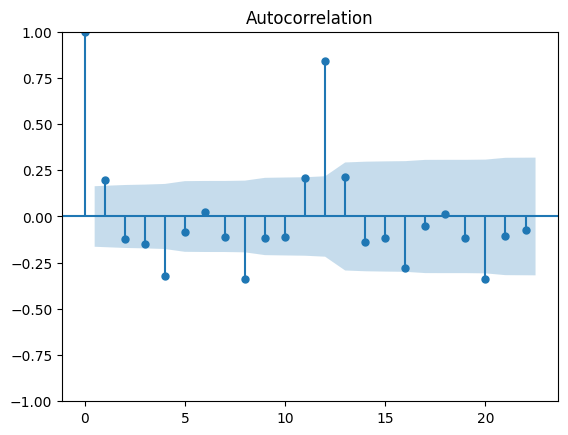
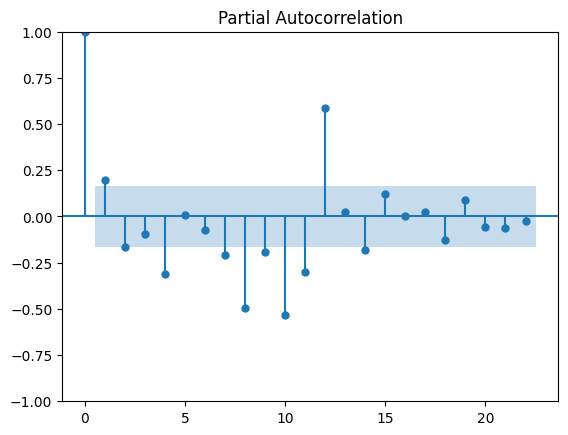
この出力の解釈ですが、lag=12について自己相関係数、偏自己相関係数ともに最も大きい値を取っており、この事から元のデータは12ヶ月という周期に対して最も相関があるという事が読み取れます。

まとめ

今回は時系列データに対する基本的な分析方法についてまとめました。
時系列データに対する操作や分析方法には通常のテーブルデータに対するものに加えて、特殊な知識を要するものが多いため、日々知識を蓄積することが肝要です。
引き続き、本ブログを通じて色々な知識を一緒に学んでいきましょう。

---